A Linear System With Three Equations And Two Variables Must Be Inconsistent
Solved 1 Point Determine If The Following Statement Is Chegg Com
A linear system with three equations and two variables must be inconsistent. We start with two pairs of equations and in each pair we eliminate the same variable. The simplest kind of linear system involves two equations and two variables. Ie the statement claims that every system of linear equations with more equations than unknowns is inconsistent.
For example the system beginalign x 1 2x 2 endalign has two equations and one unknown but is clearly consistent. There are three types of systems of linear equations in two variables and three types of solutions. In mathematics a system of linear equations or linear system is a collection of one or more linear equations involving the same set of variables.
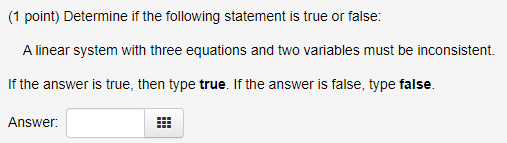
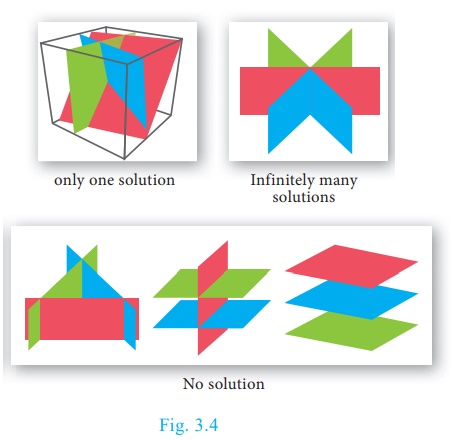
To the contrary a system with less equations than variables either is inconsistent or it has infinitely many solutions. Has three equations and two variables but infinitely many solutions. B If latexd_1d_2d_30latex then system of linear equations is known as Homogeneous linear equations which always possess at least one solution ie.
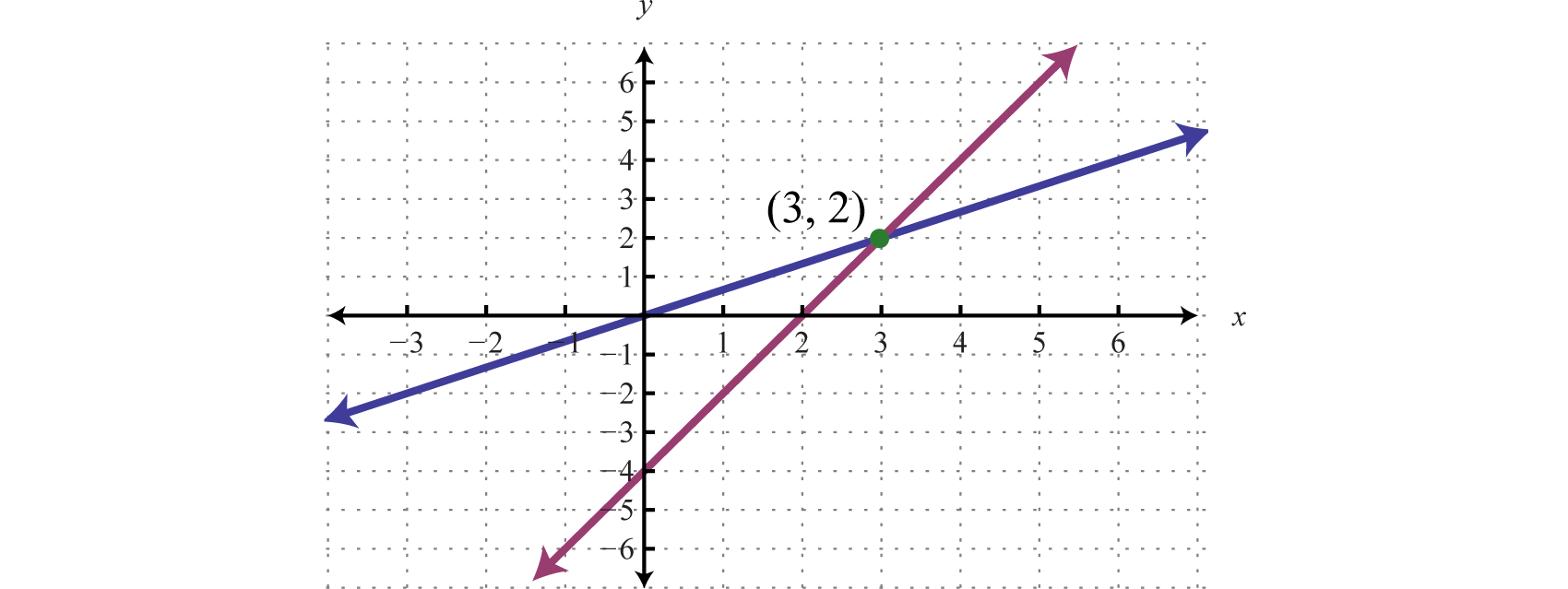
A system of equations in three variables is dependent if it has an infinite number of solutions. A A linear system of three equations in five unknowns is always consistent ie. An independent system has exactly one solution pair The point where the two lines intersect is the only solution.
The first is solving by graphing. The following linear system is consistent and contradicts the statement above. In the first example above we graphed both equations and the solution to the system was the intersection of the lines.
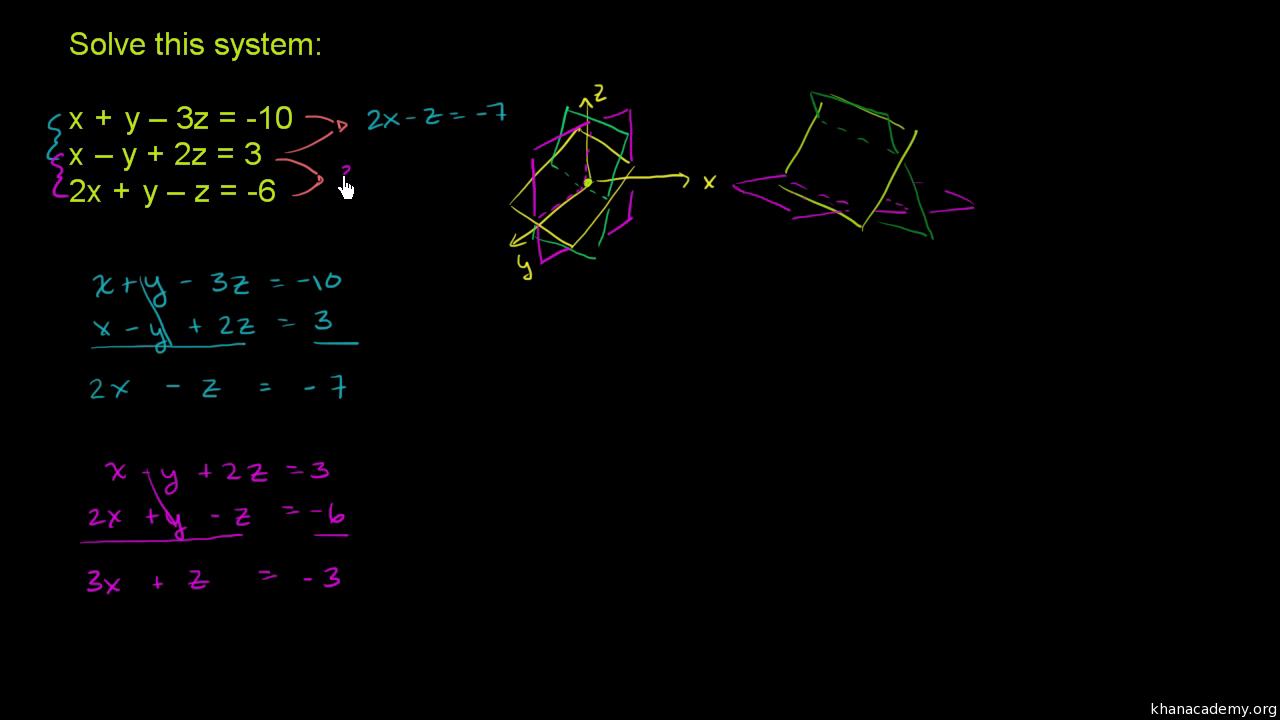
There are three common methods for solving systems of linear equations with two variables. So to recapsystem of two linear equations can have only. It is possible for three linear equations to be inconsistent even though any two of.
This will then give us a system of equations with only two variables and then we know how to solve that system. One method for solving such a system is as follows.
A Linear System With Three Equations And Two Variables Must Be Inconsistent Youtube
A Linear System With Three Equations And Two Variables Must Be Inconsistent True Or False Justify Wegglab
Solve Systems Of Equations With Three Variables Intermediate Algebra But Cloned This Time Not Imported
Solving Systems Of Linear Equations In Three Variables Using Determinants Video Lesson Transcript Study Com
Solving Systems Of Equations In 3 Variables
Systems Of Three Equations With Three Variables Are Often Called 3 By 3 Systems In General To Find A Single Solution To Any System Of Equations You Ppt Download
Lecture 14 Systems Of Linear Equations Inconsistent Systems Using Elimination By Addition Example 3 Cosmolearning Mathematics
Solving Systems Of Linear Equations With Three Variables
Solutions To Systems Of Equations Consistent Vs Inconsistent Video Khan Academy
Solving Systems Of Linear Equations With 3 Variables To Solve For Three Variables We Need A System Of Three Independent Equations Ppt Download
Solving Linear Systems In Three Variables Read Algebra Ck 12 Foundation
Inconsistent System Of Equations Definition Example Video Lesson Transcript Study Com
System Of Linear Equations In Two Variables Definition
Three Ways To Solve Systems Of Linear Equations In Two Variables
Consistency Of Linear Equations In Two And Three Variables
Systems Of Linear Equations Inconsistent Systems Using Elimination By Addition Example 1 Youtube
Three Ways To Solve Systems Of Linear Equations In Two Variables
How Many Solutions Does A System Of Linear Equations Have If There Are At Least Two Video Khan Academy
Intro To Linear Systems With 3 Variables Video Khan Academy
Inconsistent And Dependent Systems In Three Variables
Chapter 04 05 Lesson Have More Eqns Than Unknowns Does It Mean We Have Inconsistent Sys Of Eqns Youtube
Systems Of Linear Equations Three Variables College Algebra
Solving Linear Systems
1
Consistency Of Linear Equations In Two And Three Variables
Consistency Of Pair Of Linear Equations In Two Variables Types Examples
Systems Of Linear Equations Module 4 Systems Of Equations Coursera
Systems Of Equations In Two Variables Boundless Algebra
Solving Linear Systems With Three Variables
System Of Linear Equations Wikipedia
Systems Of Linear Equations Equivalence Independence Dependence Consistency
Inconsistent And Dependent Systems In Three Variables
Systems Of Equations In Two Variables Boundless Algebra
A Linear System With Three Equations And Two Variables Must Be Inconsistent True Or False Justify Wegglab
Solved 4 True False And Short Answer Questions True Or Chegg Com
Systems Of Linear Equations In Three Variables
3 4 Solving Linear Systems With Three Variables Mathematics Libretexts
Systems Of Linear Equations Two Variables College Algebra
Inconsistent And Dependent Systems In Three Variables
Solving Systems Of Equations In Three Variables Ppt Download
Systems Of Linear Equations In Three Variables
Consistency Of Pair Of Linear Equations In Two Variables Types Examples
Solve Systems Of Equations With Three Variables Intermediate Algebra But Cloned This Time Not Imported
Systems Of Equations In Two Variables Boundless Algebra
How To Solve 3 Variable Systems Of Equations Beginner S Guide By Brett Berry Math Hacks Medium
System Of Linear Equations In Three Variables Example Solution Algebra
Systems Of Linear Equations Two Variables College Algebra
Solving Linear Systems
1
A True or False.
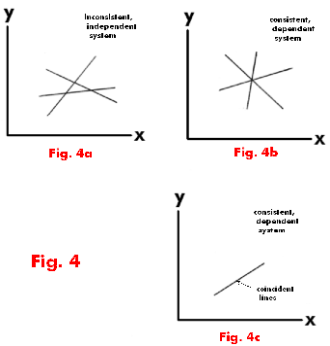
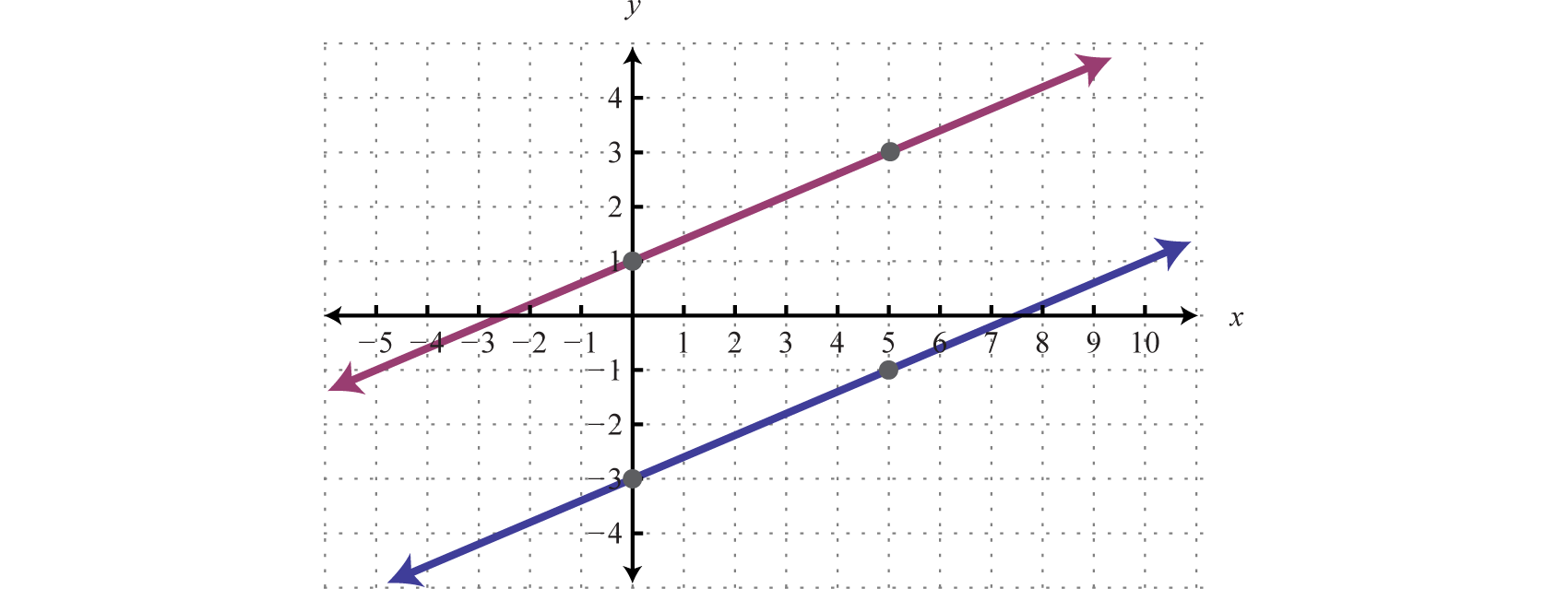
So to recapsystem of two linear equations can have only. An inconsistent system has no solution. A linear system with three equations and two variables must be inconsistent. For example the system beginalign x 1 2x 2 endalign has two equations and one unknown but is clearly consistent. All the three planes will have to parallel. In mathematics a system of linear equations or linear system is a collection of one or more linear equations involving the same set of variables. B If latexd_1d_2d_30latex then system of linear equations is known as Homogeneous linear equations which always possess at least one solution ie. A linear system with three equations and two variables must be inconsistent. Or in some cases when lines are parallel there will be no point of intersectiontherefore there will be no solutions to the system.
The system is inconsistent if at least one of the determinants D x D y or D z has a value not equal to zero and the denominator determinant has a value of zero. All the three planes will have to parallel. Systems of equations in three variables that are inconsistent could result from three parallel planes two parallel planes and one intersecting plane or three planes that intersect the other two but not at the same location. A linear system with three equations and two variables must be inconsistent. Its impossible it has a unique solution. There are three common methods for solving systems of linear equations with two variables. In mathematics a system of linear equations or linear system is a collection of one or more linear equations involving the same set of variables.
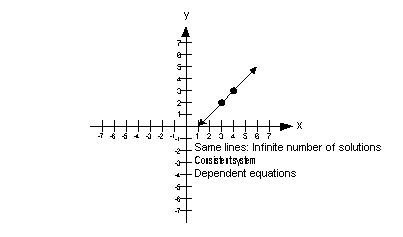
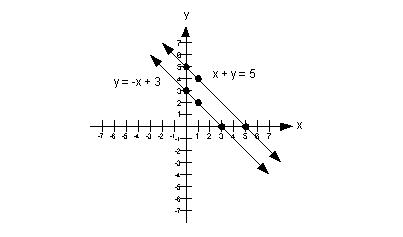
Post a Comment for "A Linear System With Three Equations And Two Variables Must Be Inconsistent"